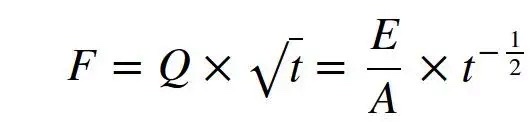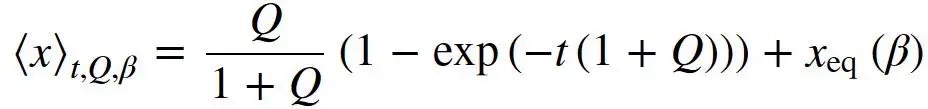辐照材料的损伤模型
近几年,损伤因子已广泛用于衡量材料经受不同水平辐射的潜在效应(粗糙化,裂纹,等等),是评估实验辐照条件下材料响应(宏观效应)的非常有用的参量。
在MRE论文“A model for defect formation in materials exposed to radiation”中,智利核能委员会(Comisión Chilena de Energía Nuclear) Sergio Davis博士等人建立了一个简单的理论模型,从经验和理论两方面,阐述了材料受辐照产生缺陷的损伤因子概念的有效性。
这是对未来使用此类有效参数的重要评估,这些参数可以用来确定实验方案和装置是否能够再现相关效应,该模型既新颖又实用。
摘要
介绍了材料辐照缺陷随机演变的简单模型。采用主方程形式,根据功率通量和辐照时间推导了平均缺陷数的表达式。该模型定量地再现了由于缺陷复合引起的自愈行为,达到了取决于入射辐射的功率通量和材料温度的稳态缺陷浓度,同时还提出了最有效产生缺陷的入射能量特定时间尺度,与实验结果一致。利用这个模型,讨论了积分损伤因子,该因子是结合功率通量和辐照时间平方的描述符。近年来,核聚变反应堆等离子体壁材料研究人员已使用该因子来测量不同类型辐射与大范围功率通量和辐照时间条件下各种类型实验中产生的等效材料损伤。积分损伤因子在实际中很实用,但缺乏正式的理论依据。研究发现,在这个简单的模型中,积分损伤因子与最大缺陷浓度成正比。
引言
辐照材料研究是一个宽泛的主题,其应用对于医学、天体物理学和核反应堆的设计至关重要。材料的辐照效应在原子和微观结构尺度上是变化的,主要取决于撞击表面的入射粒子(中性粒子、离子、电子和中子)的能量。这些效应包括加热、离子注入引起的脆化、裂纹和空隙的形成、局部熔化和再结晶或非晶化、各种类型的蒸发和烧蚀,甚至不同程度的电离。在原子水平上,辐射损伤包括点、线和体缺陷的形成:空位或间隙簇、位错环、堆垛层错、孪晶,以及堆垛层错四面体的形成。有趣的是,已经确定了几种线缺陷和体缺陷可以在原子水平上追溯到由于辐射损伤事件引起的空位和间隙缺陷的积累。
设计和建造核聚变反应堆时的一个问题是为其等离子体壁选择合适材料。基本要求是此类材料必须具有抗极端热通量和抗高通量辐射特性,辐射主要来自中子、离子束、 He 和 H 同位素(如氘)。为了测试这些材料,人们必须能够使用实验装置产生与磁约束(MC)聚变装置(如计划中的ITER 托卡马克装置)或惯性约束聚变(ICF)实验(例如在国家点火装置上进行的实验)中相似的条件。
材料在辐照条件下受到的损伤程度取决于几个变量,包括等离子体与材料相互作用的时间、峰值功率和沉积到材料中的能量。实际上,这些参量在磁约束或惯性约束聚变实验的不同环境中存在很大差异。在磁约束中,尤其是在 ITER 中,偏滤器中与 100 J/cm2–300 J/cm2 的边缘定位模式相关的能量负载预计具有 0.1 ms–0.5 ms 的持续时间,每次发射 103 个脉冲,频率为 0.5 Hz –2 Hz。在惯性约束实验条件下,腔壁上的能量负载预计为 3 J/cm2–6 J/cm2,持续时间为 0.2 µs–1 µs,频率约为5 Hz。
因此,非常需要对辐射损伤进行通用测量,以表征所有这些不同环境中的表面侵蚀。为此提出了不同的描述符,一个是积分损伤因子 (IDF),定义为
其中 Q 是功率通量,E 是沉积在区域 A 上的能量,t 是与材料相互作用的时间。实验证据表明,当 IDF 具有相同数量级时,在不同环境下会产生类似程度的材料受损。例如,当钨(i)在RHEPP 离子加速器上以 4.5 J/cm2辐照200 ns,(ii) 用 QSPA Kh-50 等离子体枪以150 J/cm2 照射0.5 ms,(iii) 在 JUDITH 电子加速器上以550 J/cm2 的能量通量辐照3 ms,在这三种情况下,IDF 为 7 kW×s1/2/cm2–10 kW×s1/2/cm2。考虑到前述ITER和惯性约束实验中的预期条件,对这两种情形,反应堆第一壁的预期 IDF因子预计约10kW×s1/2/cm2。
在其他辐照设施和设备(例如,等离子枪、电子和离子加速器、脉冲激光器)中,近年来已使用等离子聚焦 (PF) 装置来探测这些条件,因为该装置可以通过产生高功率通量密度达到相似的IDF值,从而能够研究材料损伤。经箍缩压缩后,PF装置可以产生轴向喷射的等离子体激波,当材料暴露于其中时,可以将 0.01 J/cm2–100 J/cm2 的能量集中到 10 ns–500 ns 的时间尺度,具体数值取决于从阳极到靶的距离。这些条件对应的IDF值为 1 W×s1/2/cm2–104W×s1/2/cm2 。因此,PF 放电可以产生与核聚变反应堆第一壁材料相当的IDF条件(∼10 kW×s1/2/cm2)。尽管最初使用储能为兆焦耳级的PF设备来产生这些IDF值条件,但近年来,根据定标关系已允许建造亚千焦耳和亚百焦耳PF设备,并且定标律已拓展到小于 1 J。特别是,智利核能委员会等离子体物理和核聚变实验室的研究工作表明,对于给定的离子密度、磁场、等离子体鞘层速度、阿尔文速度和温度条件,可以对PF在很宽的能量和尺寸范围内进行缩放。受这些结果的鼓舞,台面式 PF 设备可用于研究箍缩压缩后轴向喷射的等离子体激波对材料特性的影响。实验发现,通过调节光源与样品之间的距离,数百焦甚至几焦耳的台面式 PF 设备可以产生与兆焦耳PF设备相同能量密度和IDF 值的条件。通过这种方式,有望在核聚变反应堆条件下,在台面式等离子体设备上实现对等离子体壁候选材料的测试。
因此,无论效应和实验装置如何变化,似乎都有可能有一个全局描述符来估计损伤程度。从这个意义上说,IDF这一因子(F )似乎是比较不同类型实验结果的有用指标,但可惜的是,缺乏对这一经验事实的恰当的理论解释。虽然已经提出了一些论点,但显然需要从缺陷的产生和重组的原子现象中为 F 提供一个良好的理论基础。
在目前的工作中,基于连续时间主方程,我们提出了一个简单的动理学模型,用于估算给定输入功率通量 Q 和辐照时间 t 产生的缺陷比例。该模型给出理解F如何依赖于缺陷比例的良好起点,为该经验描述符提供了物理解释。
结论
我们开发了一个简单的缺陷比例动理学模型,作为输入功率通量 Q 和辐照时间 t 的函数。该模型考虑了由于入射辐射引起的缺陷产生以及由于热迁移引起的缺陷复合。有趣的是,该模型与辐射类型(例如,电子、离子、等离子体激波、热通量、电磁辐射、激光)无关,仅取决于缺陷形成的能量,而不取决于缺陷的特定类型。这样,我们得到了公式
用以表示由入射功率通量、材料温度(β )和照射时间决定的平均缺陷数。
我们预计,对于任何给定的功率通量,材料在长时间辐照后会达到稳定状态,此时由于缺陷的产生和复合之间达到平衡,因此缺陷比例保持不变。随着材料温度的升高,材料达到新的稳态,缺陷更多。本模型预期的缺陷数量与相同功率通量和曝光时间的 PF 实验中熔化的观察结果一致。
根据本模型的假设,缺陷的最大比例随着IDF的增加而增加,且在 F/F0 ∼ 0.1 (F0为构造的IDF的自然单位(Natural unit))以下这一关系大致呈线性特征,这意味着高IDF 值时缺陷的产生并不十分有效。当然,缺陷数量的最大值不能无限增加,所以可认为当缺陷浓度高于某阈值时本模型失效,此时必须考虑除缺陷形成之外的不同现象。
该模型对IDF 的描述支持对具有不同类型辐射和大范围功率通量和辐照时间的各种类型实验的观测结果。更有趣的是,它还支持使用台面式PF设备在核聚变反应堆条件下进行等离子体壁候选材料的测试。通过该方式,可能在小型实验室中进行这些台面实验,而这以前只能在大型实验装置上进行。
我们也承认本模型不包括其他类型的缺陷,例如双空位或空位簇、位错或晶界的影响。然而,它是一个新起点,使我们能够了解原子过程与在等离子体壁材料中辐射引起的损伤的宏观测量之间的联系,以及 IDF 描述符的物理意义。
论文原文:
Sergio Davis, Felipe González-Cataldo, GonzaloGutiérrez, et al. A model for defect formation inmaterials exposed to radiation. Matter and Radiation at Extremes 6, 015902(2021); https://doi.org/10.1063/5.0030158
延伸阅读:
R. Gonzalez-Arrabal, A. Rivera, and J. M.Perlado. Limitations for tungsten as plasma facing material in the diverse scenarios of the European inertial confinement fusion facility HiPER: Current status and new approaches. Matter Radiat. Extremes 5(5), 055201 (2020).https://doi.org/10.1063/5.0010954
V. A. Gribkov, I. V. Borovitskaya, E. V.Demina et al. Application of dense plasma focus devices and lasers in the radiation material sciences for the goals of inertial fusion beyond ignition. Matter Radiat. Extremes 5(4), 045403 (2020). https://doi.org/10.1063/5.0005852