
两位物理师讲述了在职业生涯中的感悟,通过跨越过去30年来质子治疗的演变历程,带领读者从质子治疗的开端走到普遍使用的当下。30年来,为提高质子治疗获益,慢慢开展了调强质子治疗和弧形治疗,从治疗计划、优化充分考虑质子特定的不确定性,利用成像方法来测量并规划患者体内的质子射程。最后讨论了通过大幅降低质子治疗的规模和价格,实现质子治疗的普及化,从而使质子治疗得以在全球范围内得到推广。
与光子放射治疗相比,粒子治疗所涉及的物理学更有趣。质子治疗也有更多的创新之处,而且随着许多新公司进入该领域,使得质子治疗更具活力。例如,虽然光子治疗中的加速器技术自20世纪70年代以来没有发生根本性变化,但质子和粒子治疗中出现了新的超紧凑型同步回旋加速器、同步加速器、高梯度直线加速器和激光尾波场加速器。通过激活氧-15和碳-11同位素达到质子“辐射手术刀”,并产生独特的瞬时伽马辐射。然后是技术方面,能够以亚毫米精度控制重100 t巨型设备的能力。质子和粒子治疗是医学领域中使用的昂贵技术,设备价值接近上亿美元。将这项技术普及化、大幅缩小其规模和价格以使更多患者能够负担得起,面临着巨大的挑战和机遇。最近的临床试验结果显示质子治疗的效果有所改善,对于试图最大限度地为患者带来益处的医学物理学家来说这非常激动人心。质子治疗在过去60多年里一直处于指数级增长的道路上,而且没有迹象表明会停止增长。
资深物理师Thomas Bortfeld博士的观点
在职业生涯的早期阶段,Thomas博士对质子治疗的益处持怀疑态度。1988年至1990年,Thomas博士在海德堡撰写了一篇关于调强放射治疗(IMRT)的逆向计划和优化的论文。Thomas博士在论文中认为,光子调强计划通过优化计划可以产生与质子剂量分布一样好或更好的剂量分布,质子治疗的支持者夸大了布拉格峰物理学优势:几乎每一本关于质子治疗的教科书和介绍性讲座都是从布拉格曲线与光子治疗中明显较低的指数型剂量跌落的一维比较开始的。然而,这种比较是有误导性的,因为放射治疗中的剂量适形问题是一个三维问题。与质子束相比,光子束的横向剂量跌落(X方向和Y方向)与质子束大致相同,甚至有时更陡峭。假设可以将许多共面或非共面射束组合起来,则在一个维度上凭借陡峭剂量边缘的能力足以雕刻出任意形状的高剂量区域匹配任何肿瘤靶体积。这源于Radon变换的理论,也是计算机断层扫描图像重建的基本原理。换句话说,布拉格峰并不是实现高剂量区剂量适形性的必要条件。由于剂量落在布拉格峰以外,因此周围健康组织的平均剂量(剂量浴)至少减少1/2。
在随后的几年里发现,大幅减少辐射剂量浴是质子束的一个重要优势,尤其是与上世纪70年代相比,患者在癌症诊断后的存活时间往往更长,这使得副作用更加难以接受。其次,放化疗和放疗联合免疫疗法等联合治疗已经成为许多类型癌症的标准治疗方法,这意味着必须重新评估正常组织中的辐射剂量阈值。Thomas博士因此改变了对布拉格峰重要性的看法,尽管不像与光子束的指数型剂量跌落的一维比较那么重要,但它仍是重要的。
1995年,Thomas博士在海德堡大学物理系以光子和质子束的理论和实际剂量适形潜力为论文方向进行了研究,这是Thomas博士在德国获得教授职位所需的第二篇博士论文。大约在同一时间开始了德国癌症研究中心和瑞士保罗谢勒研究所的密切合作,在先进的光子IMRT计划和质子治疗计划之间进行可靠的相互比较研究,见图1。这项合作变成了一场友好的竞争,将两种方式实现的计划推向了物理极限。该项研究表明,质子治疗可使剂量浴减少2/3,而不是仅仅1/2。调强对于充分利用光子和质子束的剂量适形潜力至关重要。
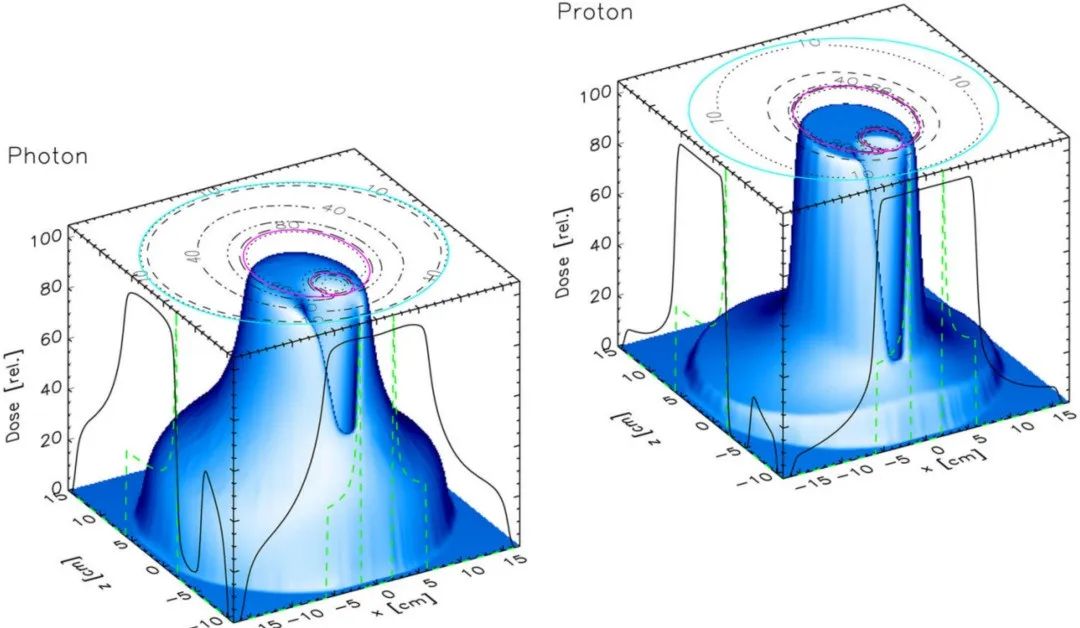
图1.光子和质子束对于包裹在危及器官周围的肿瘤靶体积的剂量适形潜力的理论极限。在这两种情况下均采用了弧形治疗和调强。质子剂量分布未考虑射程不确定性。
布拉格峰的数学之美
在20世纪90年代中期研究光子和质子剂量分布时,光子深度剂量分布的简单近似值(通常是指数型)在建模和理解光子束的剂量适形潜力方面通常很有用。另一方面,当时还不存在质子布拉格曲线的解析。然而事实证明,推导布拉格曲线的解析表达式非常简单。
根据Bethe Bloch方程,质子在正常组织中的阻止本领与质子速度的平方近似成反比,与其动能大致成反比: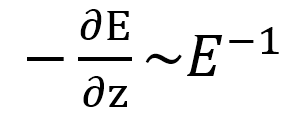 。质子减速越慢,在一定深度间隔内损失的能量就越多,这就是布拉格峰产生的全部原因。因此,能量损失-∂E对应增加深度与能量成正比:
。质子减速越慢,在一定深度间隔内损失的能量就越多,这就是布拉格峰产生的全部原因。因此,能量损失-∂E对应增加深度与能量成正比: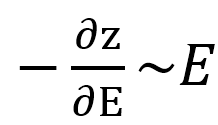 。通过积分得到能量与射程的关系:
。通过积分得到能量与射程的关系: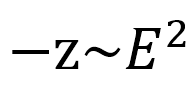 。这意味着以深度为函数的阻止本领为
。这意味着以深度为函数的阻止本领为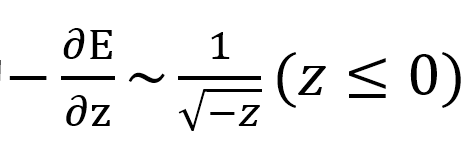 。这个推导假设所有质子都停止在相同的深度,即Z=0处。射程歧离导致射程近似高斯分布。这可以通过将上面提到的阻止本领与射程高斯离散分布卷积化来建模,以产生函数形式的布拉格曲线表达式:
。这个推导假设所有质子都停止在相同的深度,即Z=0处。射程歧离导致射程近似高斯分布。这可以通过将上面提到的阻止本领与射程高斯离散分布卷积化来建模,以产生函数形式的布拉格曲线表达式: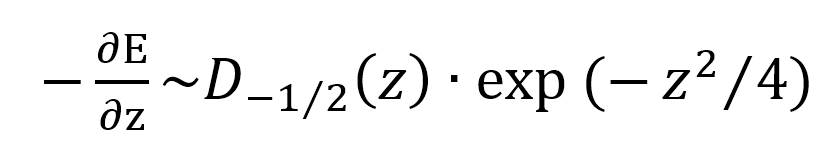 。
。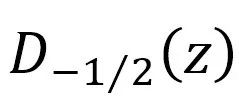 是一个特殊的抛物线柱函数。这种函数形式和布拉格峰曲线的相应形状具有独特气息,如图2所示。
是一个特殊的抛物线柱函数。这种函数形式和布拉格峰曲线的相应形状具有独特气息,如图2所示。
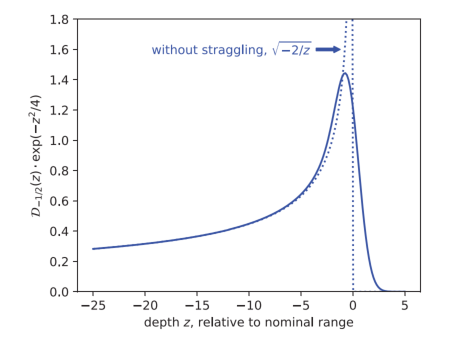
图2.布拉格峰曲线(实线)的函数形式图,以幂函数的卷积形式描述深度Z处的阻止本领,具有高斯射程离散分布。虚线展示不含射程歧离的情况。
尽管进行了许多近似和简化,但上述的简单模型相似于测量的和更精确计算的布拉格曲线。考虑到Bethe-Bloch方程中的对数项以及相对论效应,将射程—能量关系中的指数从2降低到约1.8时更明显。
抛物线柱函数和高斯函数的乘积的函数类型,称之为Q函数,其本身也有一些可用于其他应用的特征。其中一个特征是两个Q函数的卷积变成了另外一个Q函数。如快速计算通过质子束激活产生的预期正电子发射断层扫描(PET)图像,只需将剂量分布与一个Q函数进行卷积即可。在另一项研究中,通过一个Q函数与测量的PET图像进行反卷积,直接重建剂量分布。现在慢慢应用于快速伽马成像。